In his paper he basically proposes a very simple "machine" (which later on became known as the Turing Machine - TM). This TM gives us a description of what such a device can and cannot compute, thereby showing us as well that (if we take the TM as the only "object" capable of calculating things) the number of things we can't compute/calculate is infinitely larger than the number of things we can compute.

But let's forget about that infinite set of things that we can't compute and about the fact that our knowledge is so infinitely small. That's not what concerns us here.

On its own, the Turing Machine has both advantages and limitations, and consequently many alternatives to it have been proposed over the last sixty years. Very recently, a new proposal has emerged: Memcomputing.

Before going over some interesting aspects of Memcomputing, let us dive a little deeper into the topic of Turing Machines (and a couple more concepts, relevant to our discussion here).

Turing Machines

In its (almost) simplest form, the Turing machine can be visualized as follows:

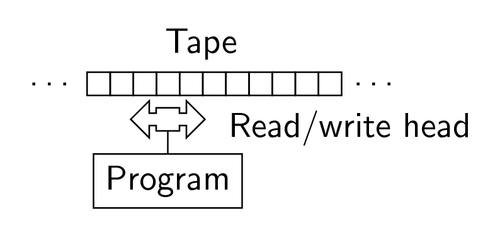
(image taken from here)

and can be understood in the following way: the Tape can have values written on it, let's say 0, 1 or Nothing. The Reader/Writer (the double-headed arrow between the Tape and the Program-box, labeled as "Read/write head") reads the value that is written in one specific cell of the Tape, and reacts to what's written there, by doing for example the following:

1. write a 0 in the cell
2. move (the whole Reader/Writer + the Program-box) one position to the left
3. change your state to Blue

(assuming than in the Program-box there is a label that indicates the "color" feature - for some inexplicable reason).

All sorts of (weird and) interesting things can be done building up from this very basic example/concept of the Turing Machine.

Based on this very basic example, one can generalize and define something called the Universal Turing Machine (UTM), and prove, based on the definition of the UTM, that many of the computers, calculators and complicated things that we use everyday can be considered somehow equivalent to a UTM.

Von Neumann - architecture

The TM is an abstraction, an ideal model of a machine that computes "things". In real life, we need something less abstract. Usually, a UTM is realized in practice through the von Neumann architecture.

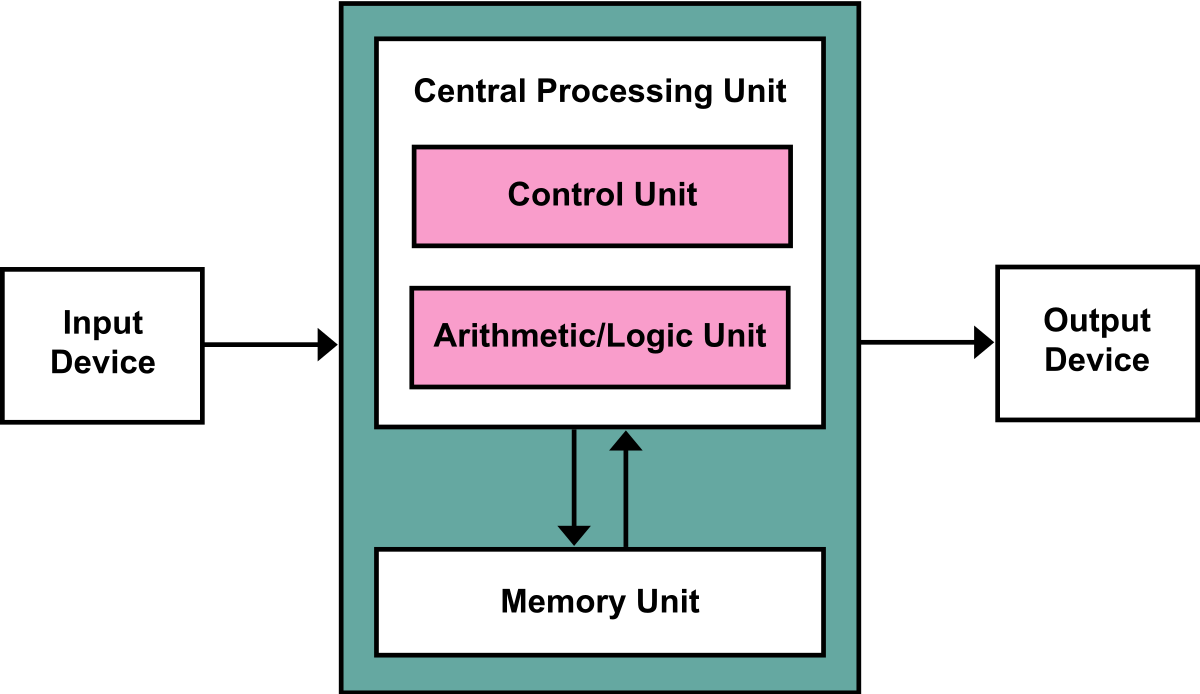
(image taken from here)

Fair enough, the picture above describing the von Neumann architecture is again an abstraction, but at least a more down to earth one. (Again, understanding the von Neumann architecture can be easy). To understand the von Neumann architecture, let's focus on its individual components:

• Central Processin Unit: like in your phone or laptop, this is the piece of electronics (buried deep within your device) that ultimately takes care of additions, multiplications, etc.
• Memory Unit: like in your phone or laptop, this would be the internal memory of your device, your SD card, etc.
• INPUT, OUTPUT: irrelevant at the moment.
• Control Unit, Arithmetic/Logic Unit: (too) specific parts of the CPU that you don't need to worry about right now.

Disclaimer: even though the von Neumann architecture is a very simplified and naive approach which suffers from many pitfalls, so don't take it too seriously, although it is indeed the original architectural base to all modern computers.

Note, in particular, how the Memory Unit and the Central Processing Unit are separated.

Memcomputing

This is the center of our discussion, with the (U)TM as its base.

Recently, a new paradigm has been proposed, an alternative to the Turing Machine that is not based on the UTM concept and inspired by the functionality of our own brain.

In 2014, Fabio Traversa and Massimiliano Di Ventra published a paper titled Universal Memcomputing Machines. In this paper they write: "Like the brain, memcomputing machines would compute with and in memory without the need of a separate CPU. The memory allows learning and adaptive capabilities, bypassing broken connections and self-organizing the computation into the solution path, much like the brain is able to sustain a certain amount of damage and still operate seamlessly".

Rather than going into the specifics let's try to motivate the idea a bit more, perhaps in simpler terms.

From an architectural point of view (architectural, in the sense of the von Neumann architecture), the authors of the paper propose a new Memcomputing Architecture:

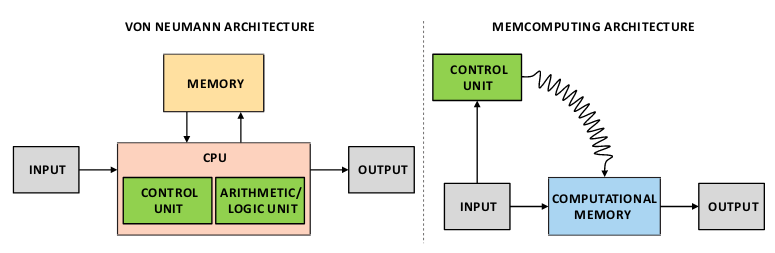
In the same way as the von Neumann architecture implements the Turing Machine, the Memcomputing Architecture implements the Memcomputing Machine. Thus raising the question: what is a Memcomputing Machine?

Think of a bottom-up approach: you can start studying the von Neumann architecture, then go and start thinking of generalizations and come up with Turing Machine (TM)-like devices, and finally go one step further and put "everything" into a single classification/framework and call it Universal Turing Machine.

Analogously, you can take the Memcomputing Architecture, start thinking of generalizations, and eventually come up with something that the authors of the paper call Universal Memcomputing Machine.

There are many details in Traversa & Di Ventra's paper, and the goal here is not to go over all of that, but rather to talk about some of the implications/claims discussed in the paper. To this end, let's divert shortly.

High Performance Computing (HPC)

It's not easy to give a definition of what High Performance Computing is. Also, you might be thinking: "everything was going so well, why muddy the waters by adding HPC to the picture?". Soon you'll see why.

For the sake of simplicity, let's assume that High Performance Computing is the same as Parallel Computing.

Parallel Computing is gathering a bunch of devices (say, your laptop or your phone) and putting them to work all together on a single task. If using one computer is good for predicting the weather next week, two must be better, right? And four even better. And so on.

Let's go back to the von Neumann architecture picture:

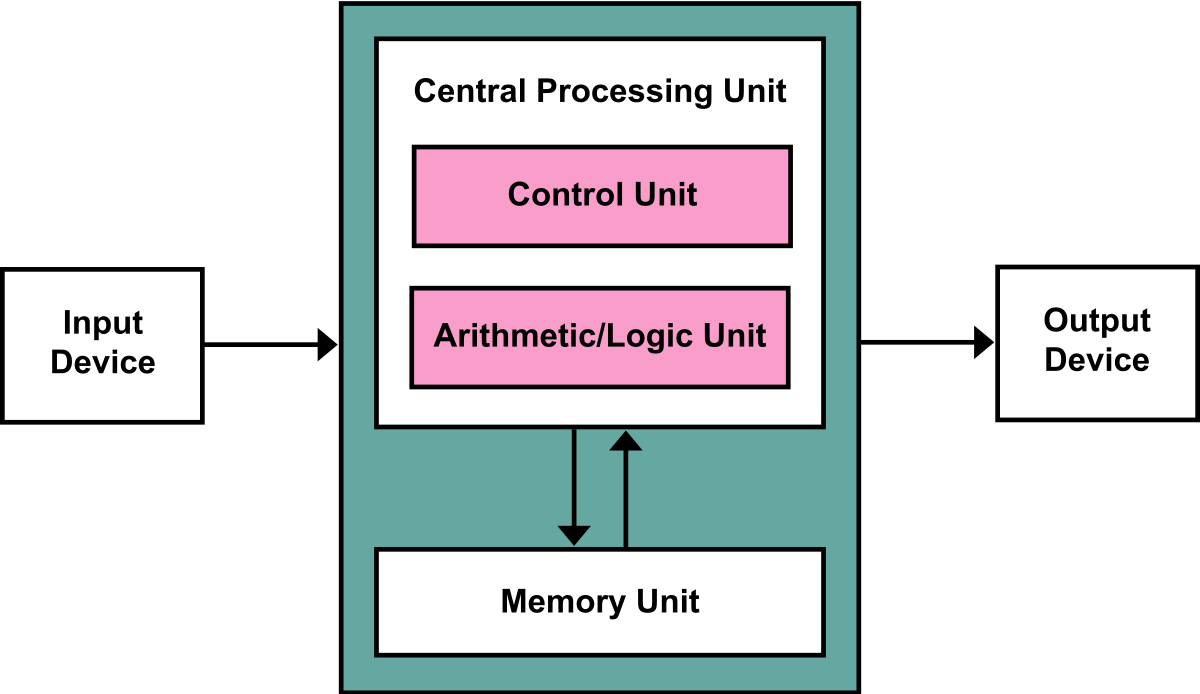
If you use a single computer for a huge problem with a lot of data (all that data stored in the Memory Unit), when the Central Processing Unit is computing stuff, it needs to bring data from the Memory Unit to calculate things. If, for the same problem, we use two computers, then each computer will have 1/2 of the total original data, and therefore less work to do.

If we use four computers, then we would have 1/4 of the problem-data for each, hence even less work for an individual computer.

But you might notice that something is off: we need to add more and more computers due to the "bad" design of the von Neumann architecture. This bad design originates (indirectly) all the way from the Turing machine: we have the Tape, which is the memory, and we have the Program-box (CPU) to decide how to "react" based on the data in the Tape.

That is how High Performance Computing comes to "save" the day. (Well, not really; it comes to alleviate some "memory pains")

Memcomputing to the rescue I: intrinsic parallelism ----> replacing HPC??

Traversa & Di Ventra claim multiple things in their proposal of a new way of doing Computer Science.

One of them is intrinsic parallelism. They claim: "the Universal Memcomputing Machine approach to parallel computing can account for a number of processing units working in parallel that can grow also exponentially, if required". That doesn't sound very clear.

Let's try again, first in pictures (image taken from here):

The idea of intrinsic parallelism is that Memcomputers are parallel in a more natural sense than the regular computers we currently know/use. Since the fundamental building-blocks of the Memcomputer are connected in some sort of network, and due to the physical properties of each of those blocks, the way information is processed in a Memcomputer has a radically different dynamics compared to our current computers, allowing for an exponentially different parallelism.

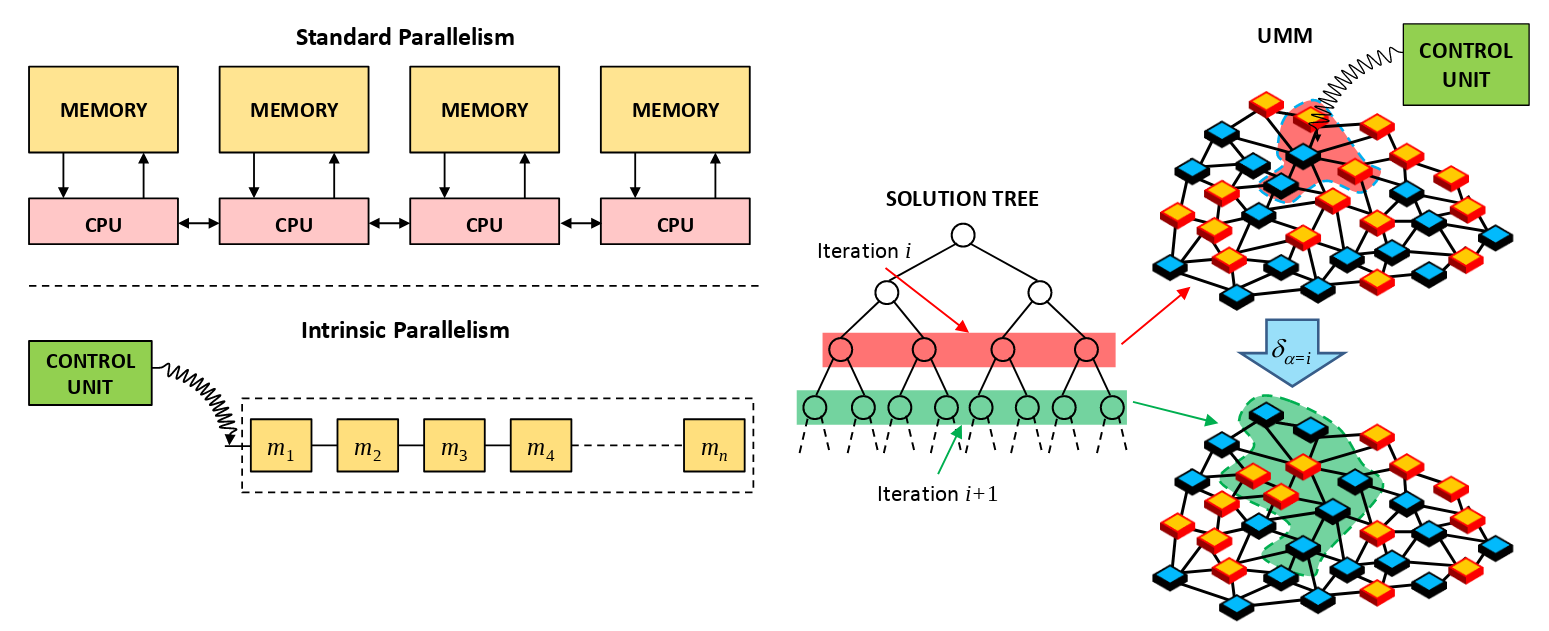
With this, Memcomputing faces the challenges of High Performance Computing from a completely new and fresh perspective.

Memcomputing to the rescue II: solving NP-complete problems in polynomial time!

A problem in Computer Science is a situation that has to be solved by means of an algorithm.

For example, sorting a list of numbers in ascending order. This is a relatively simple task, and there are many algorithms for tackling this problem. Even more, if you go from ordering a list of 10 numbers to a list of 1000 numbers, the problem can still be solved in a decent amount of time.

There are of course more complicated problems. For example, imagine you want to sell bread in your hometown. For personal reasons, you decide you want to distribute it by bike. If you have, say, 4 clients, it's not terribly complicated to figure out the fastest path to deliver bread to all of your clients.

One thing you could do (in order) to solve this bike-traveling salesperson problem, is to calculate the distance between all possible pairs of clients, and with the knowledge of your average speed on a bike, try all possible combinations and calculate all possible total distances/times, (and then decide.)

Now, going from client A to client B might not be the same as going from B to A, because the road might be steep.

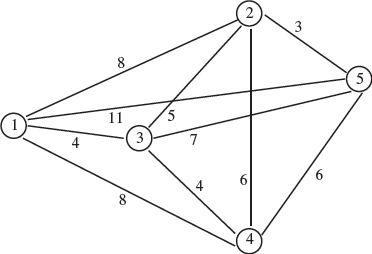
How many different paths do you have to calculate to find the shortest?

Well, the factorial function gives you the answer to this question: 4! = 24. So, in the case of 4 clients, 24 different paths. For 6 clients, 720 paths and for 9 clientes: 9! = 362880.

This is crazy. The time it takes to solve this problem (meaning, to compute all possible distances/times and then minimize) increases (insanely) rapidly with the problem size (problem size = number of clients).

Many difficult problems, such as the bread-distribution problem mentioned here, don't have a known way of being solved. We don't know how to solve them in a decent amount of time, and getting the exact correct answer. There are many ways of approximating the solution (or at least a "god enough" one) quickly, but no way of solving quickly such problems.

Traversa & Di Ventra claim that Universal Memcomputing Machines are capable of solving such difficult problems, and they show this by applying their ideas to one hard problem in particular (named the Subset-Sum problem).

Dream or reality?

Up to here, only general descriptions and claims regarding Memcomputing have been given. Want to see some criticism to this newly proposed paradigm? See this blog by Scott Aaronson.

In that article, Scott explains the physical impediments of building a Memcomputing, at least in the way proposed by Traversa & Di Ventra.

For a deeper understanding of Memcomputing, see the website of the project (http://memcpu.com/) and (their) papers listed therein (http://memcpu.com/publications/).