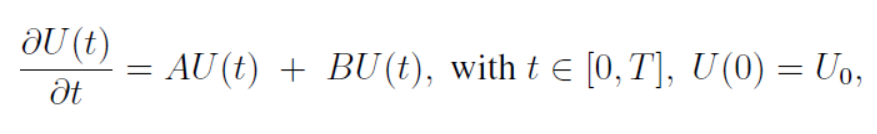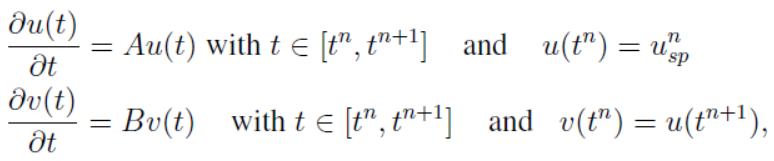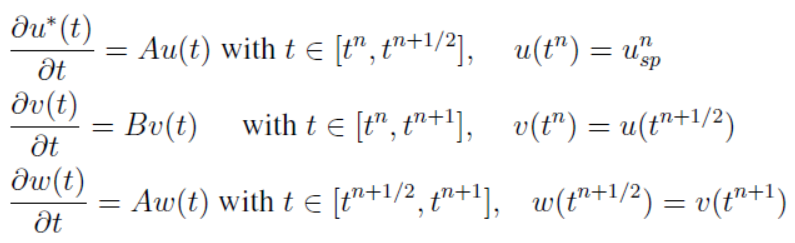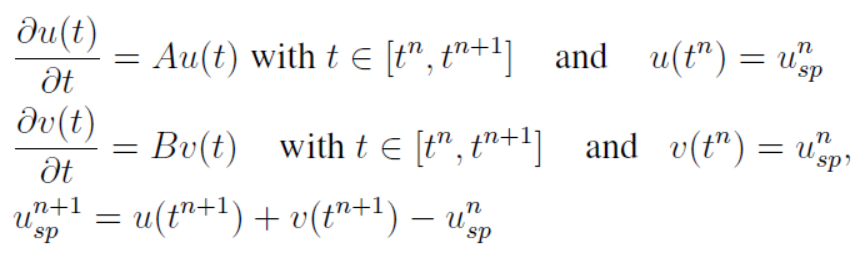Operator splitting is a powerful method for numerical investigation of complex models. The basic idea of the operator splitting methods based on splitting of complex problem into a sequence of simpler tasks, called split sub-problems. The sub operators are usually chosen with regard to different physical process. Then instead of the original problem, a sequence of sub-models is solved, which gives rise to a splitting error. In practice, splitting procedures are associated with different numerical methods for solving the sub-problems, which also causes a certain amount of error.

    Complex physical processes are frequently modelled by the systems of linear or non-linear partial differential equations. Due to the complexity of these equations, typically there is no numerical method which can provide a numerical solution that is accurate enough while taking reasonable integrational time. In order to simplify the task, operator splitting procedure has been introduced, which is widely used for solving advection-diffusion-reaction problems and Navier-Stokes equation including modelling turbulence and interfaces.

    Different algorithms like Lie-Trotter, Strang and Additive splitting were introduced to solve ODEs and PDEs. One of the simplest problems is the initial value Cauchy problem:

Lie-Trotter Splitting

Lie-Trotter splitting is a first order splitting method which solves two sub-problems sequentially on subintervals   where    and   . The different subproblems are connected via the initial conditions as follows:

where . The approximated split solution at the point   is defined as  .

Algorithm:

• Step 1:

   

  

   

• Step 2: 

   

  

   

• Step 3: 

   

  

   

• Step 4: if   , go to step 1, otherwise stop.

Strang Splitting

    One of the most popular and widely used operator splitting method is Strang splitting. By small modification it is possible to make the splitting algorithm second order accurate. The idea is that instead of first solving the first sub-problem for a full-time step, we solve it for a half time step. We then solve the second sub-problem for a full-time step, and then back to the first sub-problem and solve it for a half time step.

where   , and the approximated split solution at the point    is defined as  .

Algorithm:

• Step 1: 
  

  

   

• Step 2: 
  

  

   

• Step 3: 

   

  

• Step 4: 

   

  

   

• Step 5: if   , go to step 1, otherwise stop.

Additive Splitting

    Additive operator splitting method is a first order method and it is based on a simple idea in which we solve the different sub-problems using the same initial condition. The computed split solution of the two sub-problems is added and then the initial condition is subtracted from the sum. In this manner we obtain a splitting method where the different sub-problems have no effect on each other. This motivates the use of the additive splitting, first because the result of an additive operator splitting is independent of the order in which the operators are applied. For methods like Lie-Trotter and Strang splitting, the operators will generally not commute in the non-linear case, which means the result depends on the order in which the operators are applied. Another advantage is that the operators are applied independently, so that they can be computed in parallel.

The additive splitting algorithm is as follows:

What is next?

    In nowadays research in the field of mathematical modeling and simulations, the systems of partial differential equations are getting more complicated due to the complexity of the modeled physical, biological and engineering problems. Often, one wishes a model to capture different aspects of a situation, for instance both convective transport and dispersive oscillations on a small scale. These different aspects of the model are then reflected in a partial differential equation by different operators like diffusion or convection which are hard to analyze both theoretically and numerically, especially in the non-linear cases.  For this reason, operator splitting methods where developed.

    There are many situations in which the phenomena are modeled with more complicated system of equations than those described by PDEs. In circuit simulation, gas networks and power networks, partial differential-algebraic systems arise, but still the operator splitting methods dose not cover all the situations.

    For more details about operator splitting methods, their consistency and stability analysis, refer to: Splitting methods for partial differential equations with rough solutions. Analysis and MATLAB programs, Kenneth H. Karlsen, Knut-Andreas Lie and Henrik Risebro.